數學高考題“新”在哪兒

    ■高考典型試題解析 

    2022年新高考數學全國Ⅰ卷，被一些人認為是“史上最難”，對此我們應該冷靜而客觀地分析。其實今年高考數學除了運算量比較大之外，既無高難度的技巧，也無特別復雜的題型套路。我認為，這種“難”，其實是高考命題新理念、新變化帶給考生和教師的不適應，主要體現在四個方面。

    情境化試題使思維起點前移

    情境化是新高考命題的一大特點，此類問題求解的關鍵是“解模”，即將生活中的實際問題、探索情境轉化為數學符號語言，并借助常規的數學模型求解。若命題時將情境化試題的思維起點由“解模”前移至非連續性文本“閱讀”和數量關系梳理，就成了“數學建模”問題，其關鍵不是“解模”，而是要用數學的眼光看世界，讀懂生活中的德、智、體、美、勞，用數學的思維理解題意、建立模型。大量刷題能對“解模”熟能生巧，卻不一定對“建模”行之有效。

    比如，2022年北京卷第7題：

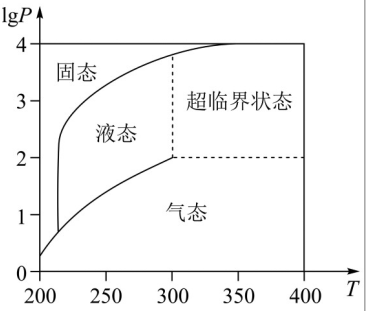
    在北京冬奧會上，國家速滑館“冰絲帶”使用高效環保的二氧化碳跨臨界直冷制冰技術，為實現綠色冬奧作出了貢獻。如圖描述了一定條件下二氧化碳所處的狀態與T和lgP的關系，其中T表示溫度，單位是K；P表示壓強，單位是bar。下列結論中正確的是（）

    A.當T=220，P=1026時，二氧化碳處于液態

    B.當T=270，P=128時，二氧化碳處于氣態

    C.當T=300，P=9987時，二氧化碳處于超臨界狀態

    D.當T=360，P=729時，二氧化碳處于超臨界狀態

    【解讀】這道題以北京冬奧會上國家速滑館“冰絲帶”使用高效環保的二氧化碳跨臨界直冷制冰技術為背景，以圖形方式給出二氧化碳所處的狀態與溫度、壓強的關系，考查考生讀圖、識圖、分析圖表數據、估值等數學應用能力。這道題創設的情境新穎，教材上沒見過，教師沒講過，考查學生對數學基礎知識、基本原理的靈活綜合運用。

    情境化問題是新高考重要的考查載體。近年高考試題用體現中國特色社會主義進入新時代的新材料、新情境、新問題，將考查內容進行“包裝”，使思維的起點由“解模”前移至“建模”。“建模”需要的是綜合能力與素養，無法像“解模”那樣總結出固定的套路供考生模仿。

    呈現方式的改變讓熟練的技能頓失用武之地

    改變呈現方式是推陳出新的重要手段，除了常規的換個說法外，將已知條件由基本量后移至導出量是一種更高層次的“推陳出新”。基本量是指在量制中約定地被認為是相互獨立的量。導出量是指由基本量根據有關公式推導出來的其他量。由基本量求解導出量，只需要借助相關的公式、定理等；由導出量求解基本量，則是較為復雜的逆向問題；由此導出量求解彼導出量，則需要基本量來中轉信息，或者依據整體思想進行整體代換——需要對各量之間的相互聯系有整體的理解與把握。大量重復的刷題訓練，主要是由基本量求解導出量，一旦面對由此導出量求解彼導出量的高考試題，考生就會感覺極不適應。

    比如，新高考全國Ⅰ卷第19題：

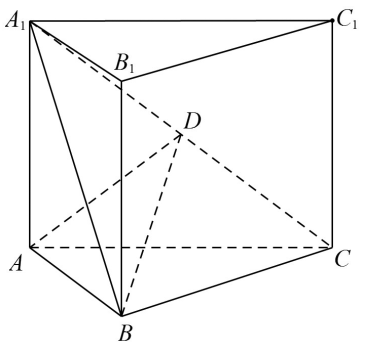
    如圖，直三棱柱ABC-A₁B₁C₁的體積為4，△A₁BC的面積為2√2。

    （1）求A到平面A₁BC的距離；

    （2）設D為A₁C的中點，AA₁=AB，平面A₁BC⊥平面ABB₁A₁，求二面角A-BD-C的正弦值。

    【解讀】本題已知量不是一些基本量，而是一些導出量：已知條件不是一維長度，而是二維面積和三維體積；已知條件不是線線垂直，而是面面垂直；已知條件不是平面角，而是空間角。

    新課標倡導整體思維，類似這樣的題目正是考查整體思維的絕佳材料。用陌生的呈現方式考查考生熟悉的問題的核心本質及其通性通法，既能考查考生的能力，又能確保公平公正。

    開放性探究性的設問有效考查考生綜合素質

    探究性、開放性試題是考查基本活動經驗與創新能力的絕佳載體，它從獨特的角度對學科知識進行多方位、深層次的考查，體現考生的個性品質和創新意識，鼓勵有獨特見解、有思想水平、有創新精神的答案。這不是考生通過大量刷題就能有效應對的，它需要考生具備必要的核心素養與關鍵能力。

    比如，全國乙卷第14題：

    過（0，0），（4，0），（-1，1），（4，2）中的三點的一個圓的方程為_____。

    【解讀】該題答案不唯一，開放的問題中蘊含了豐富的數學思維，給不同水平的考生提供了多層次的思考空間：平面內不共線的任意3點確定一個圓，但題目偏偏給出不共線的四個已知點，這讓不同層次的考生都有表現自我的機會，似乎區分度不大，但選擇的三個點不同，運算量和運算難易度不一樣。運算量大的不僅更容易算錯，而且常常造成隱性的時間丟分。該題在考查思維的靈活性和深刻性方面具有很好的選拔功能。

    開放性探究性的設問方式，鼓勵批判性思維與創造性思維，這類試題在很大程度上可以彌補封閉性試題求同思維的不足，直擊題型教學與機械刷題的痛點。

    解題路徑的創新讓題型教學束手無策

    數學是一門關于“模式”的學科——發現和使用數學模式的學科，在學習初期，題型教學和一定量的模仿訓練不僅是掌握新知識及其思想方法的必要步驟，而且還可以熟能生巧，故而很多師生都“沉迷”在這個舒適區。但在實際教學中，它存在三個嚴重問題：一是缺失題型及解題模型的生成過程，教師總是傾向于對每類問題總結出解題方法，然后讓學生直接應用，由于將大量時間花在模仿練習和記憶教師總結的分類題型上，缺失了數學模式的生成過程及解決問題的過程，造成學生對所學數學模式的認識停留于表面，在新情境中使用數學模式解題時就顯得生硬、機械，遇到新題型不知從何入手。二是題型教學和模仿訓練不是終點，更不是終極目標，僅是快速掌握新知識及其思想方法、提升核心素養和能力的載體，到了一定階段后必須脫離模仿訓練而注重思維能力提升。三是過度訓練會剝奪考生獨立思考、自由發揮的機會，訓練的結果是培養出規格型和特殊型“人才”，思維僵化，很難有創新思想，面對沒見過的高考“新題”自然就不知所措。

比如，新高考全國Ⅰ卷第22題：

    已知函數f（x）=e^x-ax和g（x）=ax-lnx有相同的最小值。

    （1）求a；

    （2）證明：存在直線y=b，其與兩條曲線y=f（x）和y=g（x）共有三個不同的交點，并且從左到右的三個交點的橫坐標成等差數列。

    【解讀】本題第二問求證三點橫坐標為等差數列，看似很復雜，如果能注意到同構式，操作起來就不會有太大的問題了。

    有些教師不注重“題型”及其通性通法的生成過程，另一方面又止步于機械的題型教學和模仿訓練，在教與學中就題論題，不對例題習題進行改編和拓展延伸，缺乏一題多變、一題多解、多題一解、多法歸一。只有對所學知識題型及其思想方法縱橫審視、反復琢磨，才可能從整體上把握數學知識內容的核心本質，才可能窺見普適性的數學思想與理性精神，從而在更高層次提升考生的核心素養與人文精神。

    面對新課標、新教材和新高考改革，如果忽視學科思維的養成，沒有形成完整的學科體系，知其然而不知其所以然，學生在考場上遇到陌生情境、陌生材料、陌生設問方式時，不能進行有效思維分析，就會自亂陣腳，無法獨立思考、靈活應變。

    （作者單位系對外經濟貿易大學附屬中學）

《中國教育報》2022年10月28日第10版